sistemas de unidades

Los sistemas de unidades:
son conjuntos de unidades convenientemente
relacionadas entre sí que se utilizan para medir diversas magnitudes (longitud, peso,
volumen, etc.). Universalmente se conocen tres sistemas de unidades: mks o sistema
internacional, cgs y Técnico. Las unidades correspondientes a las magnitudes (longitud,
tiempo y masa) expresadas en cada uno de estos sistemas, se presentan a continuación.




Las unidades de longitud:
 permiten medir el largo, ancho y alto de diferentes objetos, es decir, medidas en una sola dimensión. En el sistema internacional, la unidad de las medidas de longitud es el metro, representado por la letra m. Los submúltiplos del metro se obtienen anteponiendo a la palabra metro los prefijos: deci, centi y mili, que significan décima, centésima y milésima parte. Sirven para medir longitudes menores que el metro. Los múltiplos se forman anteponiendo los prefijos: kilo, hecto y deca, que significan mil, cien y diez respectivamente. Se utilizan para longitudes mayores que el metro. Ejemplos: 1 m es igual a 1000 mm, 1 cm es igual a 0,01 m (ver



Observe que las medidas de longitud aumentan y disminuyen de 10 en 10. Por lo tanto, para expresar una cantidad en una unidad de orden inferior (o submúltiplo) se debe dividir por el múltiplo de 10 correspondiente, sin embargo, si se quiere expresar en una unidad de orden superior se lo debe multiplicar por el múltiplo de 10 correspondiente, ejemplo, para expresar el número 975 m en km, se debe dividir 975 por 1000 (ver Tabla 1), sin embargo si se quiere expresar en cm se tiene que multiplicar 975 por 100 (ver Tabla 1).
Otros submúltiplos que son usados para medidas de longitud muy pequeñas son:
Micrómetro (μ) = 10-6 m
Nano (η) = 10-9 m.
Angstron (Ǻ) = 10-10 m.
Pico (p) = 10-12 m.
Fento (f) = 10-15 m.


Unidades de masa:

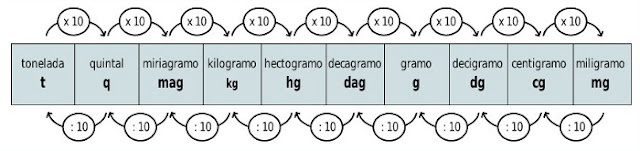
En el sistema cgs, la unidad fundamental es el gramo, que se simboliza con la letra g. Sus múltiplos y submúltiplos se presentan en la siguiente tabla. El tratamiento de los datos es equivalente al utilizado para las unidades de longitud.



Unidades de superficie:
La unidad convencional de superficie es el metro cuadrado (m2). Un metro cuadrado es la superficie de un cuadrado que tiene 1 m x 1m. Al igual que para el resto de las unidades estudiadas, existen múltiplos y submúltiplos del m2. Ejemplos: 1 m2 es igual a (103mm)2, 1 cm2 es igual a (10-2 m)2 (ver Tabla 2).
2



Unidades de volumen:
La unidad convencional de volumen es el metro cúbico (m3). Un metro cúbico es el volumen de un cubo que tiene 1 m x 1m x 1 m. Al igual que para el resto de las unidades estudiadas, existen múltiplos y submúltiplos del m3. Ejemplos: 1 m3 es igual a (103 mm)3, 1 cm3 es igual a (10-2 m)3 (ver Tabla 3).



Observe que las medidas de volumen aumentan y disminuyen de 1000 en 1000. Por lo tanto, para expresar una cantidad en una unidad de orden inferior (o submúltiplo) se debe dividir por el múltiplo de 1000 correspondiente, sin embargo, si se quiere expresar en una unidad de orden superior se lo debe multiplicar por el múltiplo

de 1000 correspondiente, ejemplo, para expresar el número 975 m3 en km3, se debe dividir 975 por 109 (ver Tabla 3), sin embargo si se quiere expresar en cm3 se tiene que multiplicar 975 por 106 (ver Tabla 3).
Otras unidades de volumen usadas habitualmente son aquellas que utilizan como unidad de volumen el litro, cuyo símbolo es l. Al igual que para las unidades de longitud, existen múltiplos y submúltiplos, para obtenerlos se usa el mismo tratamiento. Algunas de las equivalencias para tener en cuenta: 1cm3 = 1 ml; 1dm3 = 1 l, de esta manera, 1000cm3 = 1000 ml = 1l.



http://www.youtube.com/watch?v=BeieT75sTIw

notación cientifica

La notación científica: 

es un recurso matemático empleado para simplificar cálculos y representar en forma concisa números muy grandes o muy pequeños. Para hacerlo se usan potencias de diez.

Básicamente, la notación científica consiste en representar un número entero o decimal como potencia de diez.

En el sistema decimal, cualquier número real puede expresarse mediante la denominada notación científica.

Para expresar un número en notación científica identificamos la coma decimal (si la hay) y la desplazamos hacia la izquierda si el número a convertir es mayor que 10, en cambio, si el número es menor que 1 (empieza con cero coma) la desplazamos hacia la derecha tantos lugares como sea necesario para que (en ambos casos) el único dígito que quede a la izquierda de la coma esté entre 1 y 9 y que todos los otros  dígitos aparezcan a la derecha de la coma decimal.

Es más fácil entender con ejemplos:

732,5051  = 7,325051 • 10²  (movimos la coma decimal 2 lugares hacia la izquierda)

−0,005612  =  −5,612 • 10⁻³  (movimos la coma decimal 3 lugares hacia la derecha).

Nótese que la cantidad de lugares que movimos la coma (ya sea a izquierda o derecha) nos indica el exponente que tendrá la base 10 (si la coma la movemos dos lugares el exponente es 2, si lo hacemos por 3 lugares, el exponente es 3, y así sucesivamente.

Nota importante:

Siempre que movemos la coma decimal hacia la izquierda el exponente de la potencia de 10 será positivo.

Siempre que movemos la coma decimal hacia la derecha el exponente de la potencia de 10 será negativo.

Otro ejemplo, representar en notación científica: 7.856,1

1. Se desplaza la coma decimal hacia la izquierda, de tal manera que antes de ella sólo quede un dígito entero diferente de cero (entre 1 y 9), en este caso el 7.

7,8561

La coma se desplazó 3 lugares.

2. El número de cifras desplazada indica el exponente de la potencia de diez; como las cifras desplazadas son 3, la potencia es de 10³.

3. El signo del exponente es positivo si la coma decimal se desplaza a la izquierda, y es negativo si se desplaza a la derecha. Recuerda que el signo positivo en el caso de los exponentes no se anota; se sobreentiende.

Por lo tanto, la notación científica de la cantidad 7.856,1 es:

7,8561 • 10³

Operaciones con números en notación científica:

Multiplicar:

Para multiplicar se multiplican las expresiones decimales  de las notaciones científicas y se aplica producto de potencias para las potencias de base 10.

Ejemplo:

(5,24  • 10⁶) • (6,3  •  10⁸)  = 5,24 • 6,3  • 10^{6 + 8}  = 33,012 •  10¹⁴  =  3,3012¹⁵

Veamos el procedimiento en la solución de un problema:

Un tren viaja a una velocidad de 26,83 m/s, ¿qué distancia recorrerá en 1.300 s?

1. Convierte las cantidades a notación científica.

26,83 m/s  = 2,683 • 10¹  m/s

1.300 s  = 1,3 • 10³  s

2. La fórmula para calcular la distancia indica una multiplicación: distancia (d)  = velocidad (V)  x tiempo (t).

d = Vt

Reemplazamos los valores por los que tenemos en notación científica

d = (2,683 • 10¹  m/s) • (1,3 • 10³ s)

3. Se realiza la multiplicación de los valores numéricos de la notación exponencial,

(2,683 m/s) x 1,3 s  =  3,4879 m.

4. Ahora multiplicamos las potencias de base 10. Cuando se realiza una multiplicación de potencias que tienen igual base (en este caso ambas son base 10) se suman los exponentes.

(10¹) • (10³)  = 10¹⁺³  =  10⁴

5. Del procedimiento anterior se obtiene:

3,4879  •  10⁴

Por lo tanto, la distancia que recorrería el ferrocarril sería de

3,4879  • 10⁴  m

La cifra 3,4879 •  10 elevado a 4 es igual a 34.879 metros.

Dividir:

Se dividen las expresiones decimales de las notaciones científicas y se aplica división de potencias para las potencias de 10. Si es necesario, se ajusta luego el resultado como nueva notación científica.

Hagamos una división:

(5,24  • 107) (6,3  •  104)

=

(5,24  ÷ 6,3) • 107−4 = 0,831746 • 103 = 8,31746 • 10−1 • 103 = 8,31746 • 102

Suma y resta: 

Si tenemos una suma o resta (o ambas) con expresiones en notación científica, como en este ejemplo:

5,83 • 10⁹ − 7,5 • 10¹⁰  +  6,932 • 10¹²  = 

lo primero que debemos hacer es factorizar, usando como factor la más pequeña de las potencias de 10, en este caso el factor será 10⁹ (la potencia más pequeña), y factorizamos:

10⁹ (5,83  − 7,5 • 10¹  + 6,932 • 10³) = 10⁹ (5,83  −  75  +  6932)  = 6.862,83 • 10⁹

Arreglamos de nuevo el resultado para ponerlo en notación científica y nos queda:

6,86283 • 10¹²,  si eventualmente queremos redondear el número con solo dos decimales, este quedará 6,86 • 10¹².

Potenciación:

Si tenemos alguna notación científica elevada a un exponente, como por ejemplo

(3 • 10⁶)²

¿qué hacemos?

Primero elevamos (potenciamos) el 3, que está al cuadrado (3²) y en seguida multiplicamos los exponentes pues la potencia es (10⁶)², para quedar todo:

9 • 10¹²

http://www.youtube.com/watch?v=2L2CWG6ZheU